

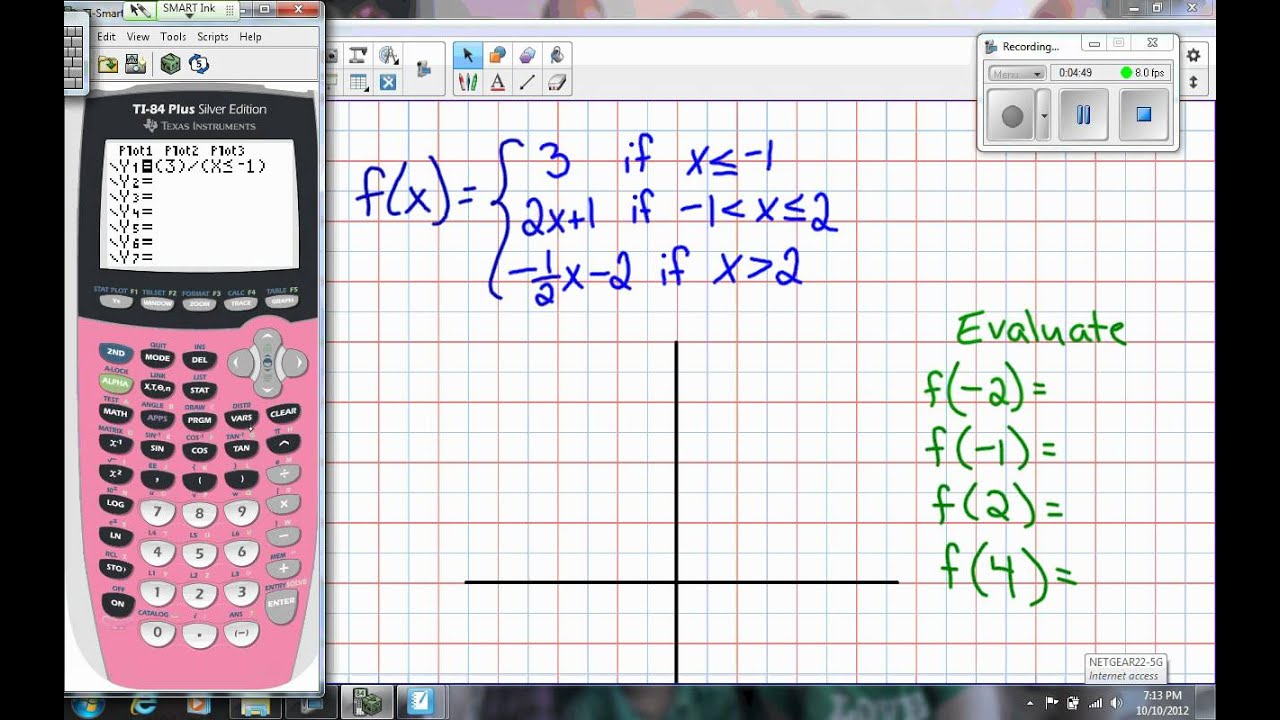
This will determine how much time you spend debriefing and practicing. At our school, this topic has been recently removed from the Algebra 2 curriculum (which explains the confused faces I saw when I asked what they remember about them from last year!). You may wish to consult with the Algebra 2 teachers at your school to determine students’ previous exposure to piecewise functions. Nevertheless, this is still considered one singular rule, just like a piecewise function is still a singular function defined in multiple ways depending on the domain. Students should be able to communicate informally that if x is between 0 and 2, the equation y=30 applies, and if x is greater than 2, y=30+10(x-2) applies. Since our number of gigabytes is variable, the rule needs to work for all possible values of x. In question 4, we purposefully use the word “rule” because we don’t expect students to know the formal notation for piecewise functions. A possible way to ask this could be: “How would the graph look different if you had to pay for a whole extra GB each time you surpassed your previous limit?” or “What if they said “$10 per additional GB or portion thereof?” Although the goal of today’s lesson is not to talk about step functions, this could be an interesting extension for groups that are ready for it. This may be different from their own actual phone plan. If students ask, clarify that you don’t need to pay for the entire extra GB if you don’t use it, and thus portions of a GB are acceptable. To make sense of the pricing structure, students first look at two concrete scenarios (question 2). Students interpret a scenario (verbal representation) and then move on to creating a graph and ultimately writing a rule (equation). In this lesson students use a pricing structure for smartphones to reason about piecewise functions.


 0 kommentar(er)
0 kommentar(er)
